
The Monty Hall problem is a classic, and let us try and deep dive into it today. Before we start, let us look at one quote that summarises the entire blog.
“The essence of strategy is choosing what not to do.” – Micheal Porter (American Academic)
Introduction
Everyone can learn from the legacy of the legendary presenter, Monty Hall. His show Let’s Make a Deal” dominated primetime in the 1960s and lasted for over 30 years. Nobody could have predicted that a harmless game show would motivate a team. A team of PhD-level statisticians and mathematicians to conduct extensive experiments. The Monty Hall issue preplexed most of us for a long time; I’m still perplexed by it.
Let me break it down for you, and then we can examine the section that’s making you confused.
Pick one of the three closed doors that Monty Hall presents to you. There is a reward behind one door and no prizes or goats behind the other two. You choose a door and announce it aloud, but you don’t immediately open it.
One of the other two doors, which you did not select,is opened by Monty, and it does not contain any gift. You have chosen one of two closed doors that are now available to you. You have no idea which of the locked doors contains the prize.
“Would you like to exchange doors?” Monty enquires.
The common belief is that the odds of winning are about the same for each closed door. You seem to have a 50/50 chance of choosing that door. Since they don’t see any benefit in switching, most people continue using the same option.
The Monty Hall Issue: Logic Explain
The moment to expose this deception with the truth has arrived. Otherwise, the Monty Hall dilemma will continue to arise. Double your chances of winning if you switch doors! (Based on statistical evidence)
Oh my gosh! The first time I heard it, I was quite shocked.
Always switching doors to the remaining door is the correct strategy for the small game. Even for a well-educated, seasoned individual, the answer seems completely counterintuitive. This occurs because, despite the availability of later revelations, the decision seems fixed. We continue to view the original option as a standalone event. The essential point is that the likelihood went from 1 out of 3 to 1 out of 2 once one door opened. It was 1 out of 3 when we started.
And if you shared that view, you’d be completely incorrect!
As for the answer, you should always switch. There are other quantitative methods to explain this. Yet the simplest one I’ve come across is this: Envision Monty presenting 100 doors instead of 3, but only one of them holds a fantastic gift. After that, the competitor picks one. Then, leaving one closed door, Monty opens 98 of the other 99 doors, each of which he finds to be useless. At this point, what is the contender to do?
With the revelation that 98 doors are useless, Monty has provided useful knowledge. It is now much more clear. So, it’s probable that the one door Monty hasn’t shown is the one holding the prize. As a result of switching, the contestant’s odds of winning increase from 1% to guaranteed.
The Logic Explained With An Example
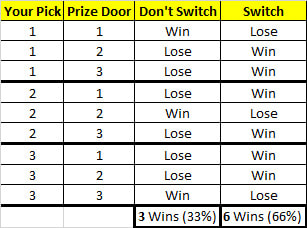
Here is an example to prove that switching does improve your chances of winning. I have computed a tiny number for each of the nine choices.
What on earth? To grasp the solution, you must first comprehend. Understand the rationale for your brain’s false assertion that the solution is 50/50. We can’t have faith in our solution. Because our minds are making faulty statistical assumptions when solving this problem.
Probabilities are usually associated with unrelated, haphazard occurrences. A nice example would be to flip a coin.Dividing the entire number of outcomes by the specific outcome yields the probability of heads as 0.5. Because of this, we believed that the last two doors had an equal chance of opening. It is not workable to have a constant probability in the Monty Hall Problem. Since the addition of extra information, the likelihood begins to fluctuate. Thus, we are mistaken.
The data in the table above shows that making your first choice is the only part that is completely at random. Choosing the right door out of the three actually only gives you a 0.33 chance of success. If you remain with your initial random decision, you’ll win 33% of the time only. As shown in the “Don’t Switch” column of the table.
This is the point that the process becomes variable. Monty isn’t picking doors at random. He’s utilising his insider knowledge to highlight the ones that are empty. Ensuring that you don’t see any doors that you haven’t picked. Neither is something happening at random nor does it have a constant chance. So, you’re completely incorrect.
Everything is wonderful and dandy, so why should I care?
There is a constant presentation of new information to make choices; thus, it matters. And it’s…dumb to remain with your previous decisions. Even when new evidence suggests they were wrong.
When fresh data from the market becomes available, companies need to make decisions. You decided on a course of action in the beginning. Because you believed it would maximise your product’s competitiveness in your market niche. Suppose, that, out of nowhere, a market disruptor arrives with a fantastic new product. How would you proceed? Will you stick with your original decision or make changes?
You’ll make a change—either by improving your product or by modifying the system. This is what the Monty Hall problem shows us. Your changes might not be a perfect fit. Yet it does show that if you don’t make it, your chances of winning are getting slimmer.
Another example that everyone may relate to is your career. When you first started working here, you painted your boss. Painted as meticulous, fascinating, and forward-thinking. Working under his supervision taught you a lot. A lot about his methods of operation, which leads you to suspect that he is a despot. What actions do you take? Do you continue working for this boss, given that you chose him before? Nope. You listen to old Monty Hall: SWITCH.
What this means is that you are not obligated to remain at door #1 because you choose it. You should be able to make course modifications. Using your experience and the outside information, SWITCH is not awful. (Except for your spouse, you keep the freedom to exchange anything.)
What Do We Learn From the Monty Hall Problem?
One thing we may learn from the Monty Hall problem. It is that probability theories can help us make better decisions and judgements. If that’s true for you, then it must be true for your company. To succeed in today’s market, one must abandon the GUT feeling and depend more on data analytics.
How is that accomplished? The next blog in this series about decision-making. It incorporates a lot of uncertainty and probability. Will focus on how Bayes Theorem works.
I hope you liked it; if so, please express your opinion by commenting 1 for like, 2 for neutral, and 3 for dislike. When you’ve fixed it, I’ll give you the choice to change it again, since one of them contains a bumper award.



Awesome piece